Optimization Process

Words Symbols

CDFs for calibration curves

memos math statistics exploration symbols

Histograms are decent visualizations for PDFs with lots of samples...

10k predictions, 20 bins

...but if there are only a few samples, the histogram-binning choices can matter a lot:

10 predictions, 4 bins
same 10 predictions, 7 bins

The binning (a) discards information, and worse, (b) is mathematically un-aesthetic.

But a CDF doesn't have this problem!

same 10 predictions, every data point precisely represented

If you make a bunch of predictions, and you want to know how well they're calibrated, classically you make a graph like this:

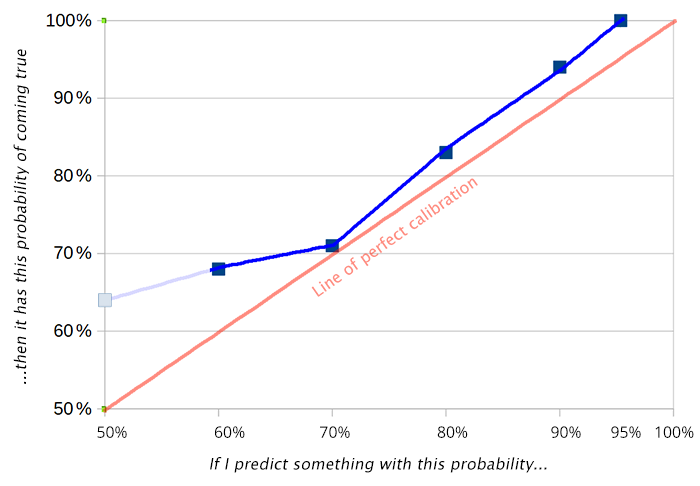
But, as with a histogram, this depends on how you bin your predictions.

100 predictions, 10 bins
same 100 predictions, 30 bins

Is there some CDF-like equivalent here? Some visualization with no free parameters?

I asked that to several people at Arbor Summer Camp. I got three answers:

  1. "You get from a PDF to a CDF by integrating. So, here, analogously, let's integrate (num predictions with confidence < x that came true) minus (expected num predictions with confidence < x that came true)."

  2. (the same thing, said in different words)

  3. (the same thing, said in different words)

If we make a "CDF" for the above 100 predictions by applying these three insights, we get:

CDF for calibration curves

.py

CDFs are a little harder to read than histograms, and I find this a little harder to read than the calibration plots above. The thing to keep in mind, I think, is: when the curve is going up, it's a sign your probabilities are too high; when it's going down, it's a sign your probabilities are too low.

Test: how would you describe the problems that these two predictors have?

Solution.